arcctg x

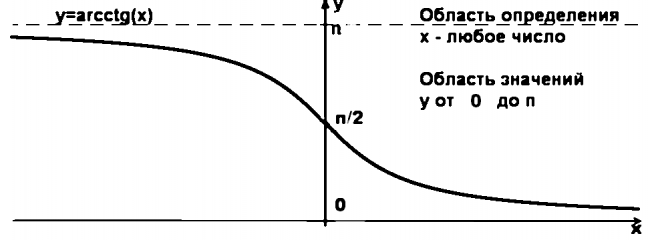
Как ведет себя арккотангенс на бесконечности? Чему равен arcctg 0? График функции y=arcctg x наглядно иллюстрирует свойства арккотангенса.

y=arcсtg x — функция, обратная y= сtg x. Область определения арккотангенса — вся числовая прямая, область значений — промежуток (0; п). Поскольку арккотангенс — непрерывная функция на всей области определения, предел арккотангенса в любой точке равен значению арккотангенса в этой точке.

$\mathop {\lim }\limits_{x \to a} arcctgx = arcctga$

В частности, так как arcctg 0=п/2, предел арккотангенса в нуле равен п/2:

$\mathop {\lim }\limits_{x \to 0} arcctgx = \frac{\pi }{2}.$

Если икс стремится к бесконечности, арккотангенс стремится к нулю, а если икс стремится к минус бесконечности, арккотангенс стремится к п. Отсюда имеем предел арккотангенса на бесконечности и минус бесконечности:

$\mathop {\lim }\limits_{x \to + \infty } arcctgx = 0;\mathop {\lim }\limits_{x \to - \infty } arcctgx = \pi .$

Добавить комментарий Отменить ответ

Свежие записи

Это интересно

Навигация по сайту

Рубрики

Свежие записи

Это интересно